
Rumus Korelasi Product Moment Pearson dan Penjelasannya

Bagi kamu yang seorang mahasiswa pastinya kamu perlu memahami bagaimana korelasi product moment pearson dimana uji ini merupakan uji parametrik untuk menguji hubungan antara 2 variable dengan skala pengukuran numerik.
Di artikel ini akan dijelaskan bagaimana cara analisis korelasi product moment pearson, cara menghitung hingga kegunaan melakukan korelasi pearson dan bagi kamu yang ingin memahami lebih lanjut yuk, simak penjelasannya berikut di bawah ini.
Analisis Korelasi Product Moment Pearson
Nah, sebelum beranjak bagaimana cara menghitung korelasi product moment pearson kamu perlu pahami terlebih dahulu analisis korelasi.
Jadi, analisis korelasi adalah bentuk interferenial yang digunakan untuk mengetahui derajat atau kekuatan hubungan, bentuk atau hubungan kausal dan hubungan timbal balik diantara variabel-variabel penelitian.
Selain itu, analisis ini dapat digunakan untuk mengetahui besarnya pengaruh suatu variabel bebas atau beberapa variabel bebas atau beberapa variabel bebas secara bersama terhadap variabel terikat melalui analisis koefisien determinasi.
Apabila terdapat hubungan antar variabel maka perubahan-perubahan yang terjadi pada salah satu variabel akan mengakibatkan terjadinya perubahan pada variabel lainnya.
Dari analisis korelasi ini dapat diketahui hubungan antar variabel tersebut, yaitu merupakan suatu hubungan kebetulan atau memang hubungan yang sebenarnya.
Jenis statistika uji hipotesis memang hubungan yang sebenarnya, dan jenis statistika uji hepotesis korelasi meliputi korelasi sederhana (bivariat), korelasi ganda, dan korelasi parsial.
Agar Mengetahui Keeratan Linear
Nah, untuk mengetahui tingkat keeratan linear antara kedua variabel yang nilainya dipengaruhi oleh skala atau satuan pengukuran pada X dan Y.
Dengan menggunakan rumus r menghasilkan koefisien korelasi akan di peroleh kemungkinan pancaran data yang diwakilinya sebagai berikut.
- Nilai korelasi yang bernilai antara -1 dan 1 yang menunjukan korelasi sempurna
- Tanda r yang menunjukan korelasi positif atau negative yang menunjukkan korelasi positif atau negative, yang menunjukan hubungan kedua penuh variabel
- Besarnya nilai r menunjukan keeratan hubungan linear antara dua pilihan
Nah, itu cara mengetahui keeratan linear dari korelasi product moment pearson yang sedikit jenisnya. Sedangkan jika banyak jenisnya kamu bisa simak penjelasan analisis korelasi yang banyak jenisnya di bawah ini.
Kurang lebih ada sembilan jenis korelasi yaitu, dan berikut penjelasan lengkapnya, yaitu:
- Korelasi perason product Moment (r)
- Korelasi ration (y)
- Korelasi Spearman Rank atau Rhi (rs atau P)
- Korelasi Bererial (rb)
- Korelasi Korelasi Poin Berserial (rpb)
- Korelasi Phi (0)
- Korelasi Tetrachoric (r1)
- Korelasi Kontigency (C)
- Korelasi Kendall’s Tau
Dan untuk membedakan korelasi yang akan digunakan, semua itu tergantung pada jenis data yang dihubungkan.
Rumus Korelasi Product Moment Pearson
Nah, selanjutnya mari kita bahas topik utama dari pembahasan artikel ini yaitu rumus korelasi product moment pearson. Korelasi product moment pearson ini bisa di sebut dengan simbol (r) dan yang paling populer dan sring digunakan oleh mahasiswa dan peneliti.
Korelasi ini dikemukakan oleh Karl Pearson tahun 1900 dan fungsi dari korelasi ini adalah untuk mengetahui derajat hubungan dan kontribusi variabel bebas (independent) dengan variabel terikat (dependent).
Dan teknik analisis korelasi product moment pearson ini termasuk teknik statistik parametrik yang menggunakan data interval dan ratio dengan persyaratan tertentu.
Sebagai contohnya adalah ketika data dipilih secara acak atau random kemudian datanya berdistribusi normal, data yang dihubungkan berpola linier dan data dihubungkan mempunyai pasangan yang sama sesuai dengan subjek yang sama.
Dan jika semua syarat itu terpenuhi, maka korelasi ini bisa digunakan, namun jika salah satu tidak terpenuhi, maka analisis ini tidak bisa dilakukan adapun rumus dari korelasi product moment pearson sebagai berikut:
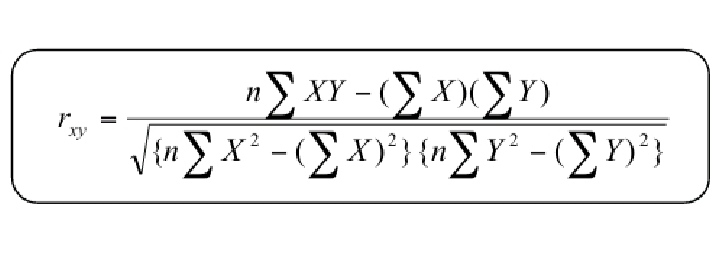
Korelasi product moment pearson ini dilambangkan (r) dengan ketentuan bahwa r tidak lebih dari harga (-1< r < 1) dan apabila nilai r = -1 artinya korelasi negatif sempurna. Dan jika r = 1 berarti korelasinya sangat kuat.
Sedangkan arti r akan dikonsultasikan dengan tabel interprestasi nilai r sebagai berikut interprestasi koefisien korelasi Nilai r.
| Interval Koefisien | Tingkat Hubungan |
| 0,80 – 1,000 | Sangat Kuat |
| 0,60 – 0,799 | Kuat |
| 0,40 – 0,599 | Cukup Kuat |
| 0,20 – 0399 | Rendah |
| 0,00 – 0,199 | Sangat rendah |
Rumus Koefisien Determinasi (R)
Setelah diujikan pada korelasi product moment pearson, kemudian nilai r itu bisa digunakan untuk menyatakan besar kecilnya hubungan variabel X terhadap Y.
Artinya pada koefisien determinasi ini bisa digunakan untuk mengetahui seberapa besar variabel Y di pengaruhi oleh variabel X yang diujikan pada data tersebut.
Koefisien determinasi bisa dinyataan sebagai seberapa besar kemampuan semua variabel bebas (X) dalam menjelaskan varians dari avriabel terikatnya (Y).
Dan secara sederhananya koefisien determinasi ini dihitung mengkuadratkan nilai korelasinya (r), sehingga dapat dirumuskan sebagai berikut.
KD = R = r2 x 100%
Keterangan
KD (R) = Nilai Koefisien Determinasi
R = Nilai Koefisien Korelasi
Dengan begitu penggunaan R Square (R Kuadrat) sering menimbulkan permaslahan, yaitu bahwa nilainya akan selalu meingkatkan dengan adanya penambahan variabel bebas dalam suatu odel.
Dan hal ini akan menimbulkan bias karena jika ingin memperoleh model dengan R tinggi seorang peneliti dapat dengan sembarangan menambahkan variabel beba dan nilai R akan meningkat.
Hal ini tidak tergantung apakah variabel bebas tambahan itu berhubungan dengan variabel terikat atau tidak
Lalu bagaimana cara pengujian hepotesanya? Kamu bisa menggunakan Pengujian Hipotesis (Uji t). Setelah mengetahui hasil korelasi (r) kemudian dilanjutkan dengan R atau determinasi, maka langkah selanjutnya yaitu pengujian signifikan.
Dan hal ini berguna apabila peneliti ingin mencari makna hubungan atau korelasi antara variabel X terhadap variabel Y.
Dan berikut merupakan rumus uji nya adalah uji t yaitu sebagai berikut:
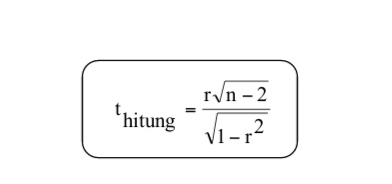
thitung =
Keterangan
thitung = nilai t
r = nilai Koefisien Korelasi
n = Jumlah Sempel
Asumsi Klasik Uji Pearson Product Moment
Syarat atau asumsi klasik untuk uji product moment pearson antara lain adalah Linearitas, Normallitas, heteroskedastisitas. Untuk mengerti asumsi klasik di atas, silahkan baca artikel kami yang relevan dengan asumsi tersebut.
Demikian penjelasan mengenai korelasi product moment pearson di artikel kami semoga bermanfaat bagi para pembaca yang memang sedang membutuhkan artikel ini.
Kesimpulan
Jadi, dapat disimpulkan bahwa korelasi Product Moment pearson ini merupakan salah satu dari beberapa jenis uji korelasi yang digunakan untuk mengetahui derajat keeratan hubungan 2 variabel yang berskala interval atau rasio.
Dimana dengan uji ini akan mengembalikan nilai koefisien korelasi yang nilainya berkisar -1, 0 dan 1. Dan korelasi ini berfungsi untuk mengukur keeratan hubungan secara linier antara dua variabel yang mempunyai distribusi data normal.
Serta untuk mengetahui diantara dua variabel terdapat hubungan atau tidak, dan jika ada hubungan bagaimana arah hubungan dan seberapa besar hubungan tersebut.








