
Pengertian, Rumus dan Penerapan Persamaan Fungsi Kuadrat
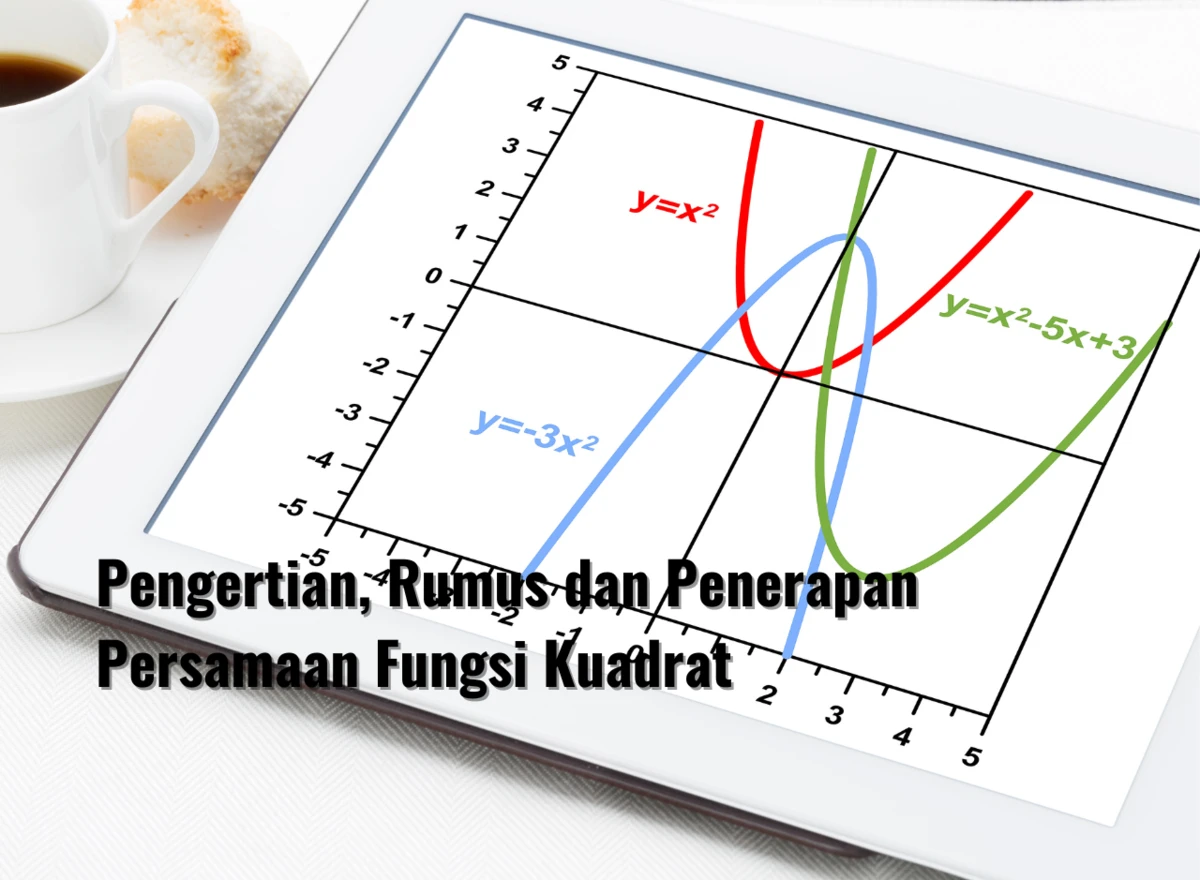
Ada beberapa macam jenis Persamaan Fungsi Kuadrat yang memiliki variabel dengan pangkat tertinggi 2.
Beberapa rumus yang harus kamu hafal untuk memecahkan penyelesaian masalah sebuah persamaan kuadrat, untuk memahami lebih mendalam mengenai pembahasan Persamaan Fungsi Kuadrat simak sampai selesai dalam artikel Media Mustakim yang di bahas pada kesempatankah kali ini.
Pengertian Persamaan Fungsi Kuadrat
Sebelum tahu pengertian Fungsi Kuadrat maka kita jelaskan dari awal, kuadrat merupakan bilangan yang berpangkat dua, sedangkan akar kuadrat yaitu bilangan dengan pangkat dua, X²=y. Artinya bilangan X sama dengan bilangan Y, jika di kuadratkan hasilnya kali dari bilangan itu sendiri sama dengan Y.
Bentuk kuadrat memuat persamaan pada pangkat tertinggi yaitu dua dengan begitu disebut persamaan kuadrat. Rumus Persamaan kuadrat ax²+bx+c=0. Sedangkan Fungsi Kuadrat adalah fungsi polynomial yang memiliki variabel dengan pangkat tertinggi yaitu dua.
Sehingga bentuk umum dari fungsi kuadrat menyerupai bentuk persamaan kuadrat. Rumus bentuk Persamaan Fungsi Kuadrat f(X) ax²+ bx²+c =0. Oleh karena itu persamaan kuadrat dan fungsi kuadrat berbeda, meski memiliki variable dengan pangkat 2 tapi berbeda pada nilai variabel nya itu sendiri.
Perbedaan Persamaan Fungsi Kuadrat
Perbedaan dari Persamaan kuadrat dan fungsi kuadrat yaitu terletak pada nilai variabelnya, karena persamaan kuadrat memiliki hasil dari penyelesaian persamaan kuadrat memiliki nilai terbatas sedangkan fungsi kuadrat tidak memiliki nilai variabel hasil dalam penyelesaiannya nilai tidak terbatas.
Sehingga nilai X dalam fungsi kuadrat dapat digantikan dengan memasukkan sembarangan bilangan dalam sebuah grafik atau juga kurva.
Rumus Persamaan Kuadrat
Rumus persamaan kuadrat ax² + bx + c = 0. Pengertiannya a, b dan c merupakan bilangan real sedangkan X merupakan nilai yang belum diketahui atau juga disebut dengan variabel yang belum memenuhi nilai persamaan kuadrat.
Rumus Fungsi Kuadrat
Berikut rumus fungsi kuadrat dan pengertiannya.
Rumus fungsi kuadrat yang sudah tidak asing lagi kita ketahui yaitu f(x) = ax² + bx+c. Keterangan F(x) merupakan = Fungsi Kuadrat, x merupakan variabel, a dan b= koefisien, c merupakan konstanta dan a= 0
Jenis-jenis Fungsi Kuadrat
Ada beberapa jenis fungsi kuadrat yang perlu diketahui diantaranya sebagai berikut di bawah ini;
- Jika Y= ax2+bx+c maka nilai b dan c adalah 0 dan memiliki fungsi kuadrat yaitu Y=ax2. Membuat grafik dengan fungsi tersebut simetris pada x=0 yang memiliki puncak di titik 0,0.
- Jika pada Y = ax2 + bx + c nilai b 0, maka akan memiliki fungsi kuadrat menjadi Y=ax2+c, yang akan membuat grafik pada fungs tersebut simetris pada x = 0 dan akan memiliki puncak di titik (0,c.)
- Dan jika titik puncak berada di titik h,k maka fungsi kuadrat akan menjadi Y=a(x-h)2+k.
Ciri-ciri Fungsi Kuadrat
Bentuk umum dari fungsi kuadrat yang hampir sama dengan persamaan kuadrat yang membedakan hanya nilai variabelnya sendiri, oleh karena itu maka kenali ciri-ciri dari fungsi kuadrat sebagai berikut di bawah ini;
- Bentuk umum dari fungsi kuadrat yaitu f(x) = ax² + BC+C dan nilai a tidak boleh sama dengan nol.
- Jika di plotkan dalam koordinasi kartesian bentuk grafiknya yaitu parabola dan bentuk dasanya U yang bisa membuka ke atas dan ke bawah tergantung pada nilai a.
- Ciri-ciri selanjutnya yaitu akan terdapat sumbu simetri memotong prabola secara vertikal
- Memiliki titik balik maksimum dan minimum
- Memiliki diskriminan dengan rumus D=b²=4ac
Penerapan Persamaan Kuadrat Pada Kehidupan
Persamaan kuadrat dalam kehidupan dapat kita temui, seperti bentuk kurva, parabola, pelangi dan yang lainnya. untuk lebih jelasnya persamaan kuadrat dalam kehidupan dapat diperhatikan berikut di bawah ini;
Persamaan Kuadrat pada Bentuk Pelangi
Pelangi yang sudah tidak asing lagi bagi manusia karena selain dengan bentuknya yang indah juga memiliki banyak warna sehingga terlihat begitu indah. Bentuk pelangi yang melengkung sehingga dapat diterapkan dalam persamaan kuadrat.
Persamaan Kuadrat pada Tendangan Arah Bola
Ketika bola ditendang maka bola akan meluncur dan akan terlihat membentuk sebuah kurva. Jadi gerakan tersebut yang merupakan salah satu penerapan dari persamaan kuadrat sedangkan gaya tendangan bola merupakan variabel.
Persamaan kuadrat Gerak Busur Panah
Gerak busur panah ketika di tarik kemudian dilepaskan maka akan terlihat seperti sebuah kurva. Arah busur panah tersebut maka akan termasuk menjadi bentuk persamaan kuadrat.
Persamaan kuadrat pada Lemparan dan Memukul Bola Baseball
Persamaan kuadrat dalam lemparan memukul bola baseball jika diperhatikan maka akan membentuk sebuah kurva selain itu grafik juga akan terlihat saat bola melambung dan tangkapan bolla akan terlihat pada polanya.
Cara Menyelesaikan Persamaan Kuadrat
Dalam menyelesaikan persamaan kuadrat ada beberapa cara yang bisa dipakai, dalam menentukan nilai x dengan pemenuhan persamaan bentuk kuadrat.
Dan hasilnya akan didapatkan yaitu subtitusi sama dengan nol. Lalu disebut dengan akar persamaan kuadrat , Akar-akar tersebut setidaknya akan menemukan tiga akar persamaan kuadrat.







